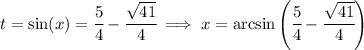Solve 5 \tan(x) + 2 \cos(x) = 0 for 0 < x < 2\pi

Question

Solve

`5 \tan(x) + 2 \cos(x) = 0`
for

`0 < x < 2\pi`

Answer 1

Rewrite the equation by using the definition of the tangent function:

`\cfrac{5\sin(x)}{\cos(x)} + 2\cos(x) = 0`

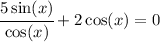
Since there is a cosine at the denominator, it can't be zero. So, we know that

`\cos(x) \\eq 0 \implies x \\otin \left\{\cfrac{\pi}{2},\ \cfrac{3\pi}{2}\right\}`

With this restriciton, let's multiply the whole equation by cos(x):

`5\sin(x) + 2\cos^2(x) = 0`

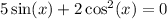
We don't like having sine and cosine in the same equation. We can fix this by using the fundamental identity of trigonometry to express cos^2 in terms of sin^2:

`\cos^2(x)+\sin^2(x)=1 \implies \cos^2(x) = 1-\sin^2(x)`

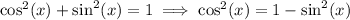
The equation becomes

`5\sin(x) + 2(1-\sin^2(x)) = 0`

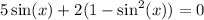
which you can rearrange as

`5\sin(x) + 2-2\sin^2(x) = 0 \iff 2\sin^2(x)-5\sin(x)-2 = 0`

This is a quadratic equation is sin(x): if you let t=sin(x) the equation becomes

`2t^2-5t-2 = 0`

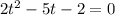
which yields solutions

`t = \cfrac{5}{4} - \cfrac{√(41)}{4},\quad t = \cfrac{5}{4} + \cfrac{√(41)}{4}`

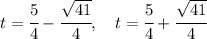
Now, remember that t is sin(x), and as such it can't exceed the interval [-1,1]. Since the second solution is greater than 1, we can only accept the first solution. So, we have

`t = \sin(x) = \cfrac{5}{4} - \cfrac{√(41)}{4} \implies x = \arcsin\left(\cfrac{5}{4} - \cfrac{√(41)}{4}\right)`