Question

You're a manager in a company that produces rocket ships. Machine A and Machine B both produce cockpits and propulsion systems. Machine A and Machine B produce cockpits at the same rate, and they produce propulsion systems at the same rate. Machine A ran for 26 hours and produced 4 cockpits and 6 propulsion systems. Machine B ran for 56 hours and produced 8 cockpits and 12 propulsion systems. We use a system of linear equations in two variables. Can we solve for a unique amount of time that it takes each machine to produce a cockpit and to produce a propulsion system?

Answer 1

We are unable to solve for a unique amount of time for each machine to produce a cockpit and a propulsion system because the system of linear equations derived from the given information is dependent, resulting in an infinite number of solutions.

Step-by-step explanation:

Given that Machine A and Machine B produce cockpits and propulsion systems at the same rate, we can establish a system of linear equations to determine the time it takes for each machine to produce a single cockpit and a single propulsion system. Let x be the time it takes to produce one cockpit and y be the time it takes to produce one propulsion system. From Machine A's output, we have:
4x + 6y = 26 ...(1)
From Machine B's output, we have:
8x + 12y = 56 ...(2)

Upon observing equations (1) and (2), we can see that equation (2) is exactly twice that of equation (1), which suggests that these equations are not independent and thus provide the same information. Therefore, they represent the same line in a Cartesian plane. As a result, there is an infinite number of solutions for x and y, and we cannot solve for a unique amount of time for producing cockpits and propulsion systems.

Answer 2

No you cannot.

Step-by-step explanation:

Let c be the amount of time it takes each machine to make 1 cockpit, and p be the amount of time it takes each machine to make 1 propulsion system.

For Machine A, we have 4 cockpits; this would take 4c time. We also have 6 propulsion systems; this would take 6p time. Together it takes 26 hours; this would give us

4c+6p=26.

For Machine B, we have 8 cockpits; this would take 8c time. We also have 12 propulsion systems; this would take 12p time. Together it takes 56 hours; this would give us

8c+12p=56

This gives us the system

`\left \{ {{4c+6p=26} \atop {8c+12p=56}} \right.`

To solve this, we want the coefficients of one of the variables to be the same. To make the coefficients of c the same, we can multiply the top equation by 2:

`\left \{ {{2(4c+6p=26)} \atop {8c+12p=56}} \right. \\\\\left \{ {{8c+12p=52} \atop {8c+12p=56}} \right.`

To cancel c, we will subtract the second equation from the first one. However, this also cancels p:

`\left \{ {{8c+12p=52} \atop {-(8c+12p=56)}} \right. \\\\0+0=-4\\0=-4`

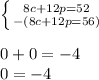
We get a statement that is not true; thus the system has no solution, and we cannot solve for a unique amount of time.