Question

The half-life for the first-order decomposition of a is 355 s. how much time must elapse for the concentration of a to decrease to

a.one-fourth

Answer 1

Given the half life of the first order decomposition reaction is 355 s

Rate constant of the first order reaction is related to the half life by the equation,

`k = \frac{0.693}{t_{(1)/(2)}}`

`k = (0.693)/(355 s)`

k = 0.00195
`s^(-1)`

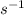
The concentration of the substance is decreased to 1/4 th.

If we start with 1 M solution, after time t the concentration becomes 1/4th = 0.25 M

First order rate law:

`[A] = [A]_(0) e^(-kt)`

`[A] = 0.25 M`

`[A]_(0) = 1 M`

`k = 0.00195 s^(-1)`

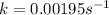
Plugging in the values to solve for t,

`0.25 M = 1 M (e^{-(0.00195s^(-1))t})`

`ln((0.25)/(1)) = - (0.00195 s^(-1))(t)`

`t = (ln(0.25))/(0.00195) s`

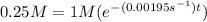
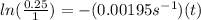
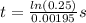
t = 710 s