Question

B. a student attaches a nozzle with an exit radius that is n times smaller than the faucet radius. 2b) let n = 3 i. how will this affect the flow rate? be specific in your explanation. (3 pts) ii. how will this affect the velocity of the water? be specific in your explanation. (3 pts)

Answer 1

Part a)

Flow rate is defined as rate of volume flow

it is determined by

`Q = (dV)/(dt)`

now if the radius of pipe is reduced then we assume here that liquid flow is ideal flow here and there is no change in the density of liquid.

So here we know that since mass is always conserved

so

`(dm)/(dt)_(in) = (dm)/(dt)_(out)`

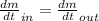
so we have

`\rho(dV)/(dt)_(in) = \rho(dV)/(dt)_(out)`

`(dV)/(dt)_(in) = (dV)/(dt)_(out)`

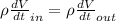
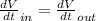
now we can say from above equation that there is no effect on the flow rate is we change the radius of pipe

Part b)

now in order to find the speed of flow'

`(dV)/(dt)_(in) = (dV)/(dt)_(out)`

`A_(in)v_(in) = A_(out)v_(out)`

`\pi r^2 v_(in) = \pi ((r)/(n))^2 v_(out)`

`v_(in) = (v_(out))/(n^2)`

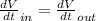
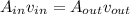
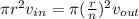
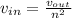
so final speed will be

`v_(out) = n^2 v_(in)`

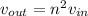
here we have n = 3

`v_(out) = 9* v_(in)`

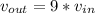
so flow speed will be 9 times more than initial speed