Question

Solve this problem please

Answer 1

The formula for depreciation is:

`y=x(1-r)^t`

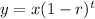
Where x = Initial value,

y= Amount after depreciation.

r= Rate of depreciation,

t = time (in years)

According to given problem,

x = 1040, y= 944 and t = 12 months =1 year.

So, first step is to plug in these values in the above formula, So,

`944 = 1040(1-r)^1`

944 = 1040 (1 -r)

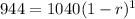
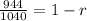`(944)/(1040) =1-r` Divide each sides by 1040.

0.907692308 =1 - r

0.907692308 - 1 = -r Subtract 1 from each sides.

-0.092307692 = -r

So, r = 0.09 or 9%.

Now plug in 0.09 in the above equation to get the depreciation equation. So,

`y = x (1- 0.09)^t`

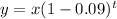
So,
`y = 0.91x^t`

b) To find the value of the bike after 5 months,

plug in t = 5 months= 5/12 = 0.41667 years in the above equation of depreciation.

So,
`y= 1040 *(0.91)^(0.41667)`

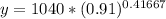
y = 1040 * 0.961465659

y = 999.9242852

y = 1000 (Rounded to nearest integer).

Hence, the value of the bike after 5 months is $1000.