Please help. 24 points!! The inverse of f(x) = (2x-1)/(x+5) may be written in the form f^(-1)(x)=(ax+b)/(cx+d)[]/tex, where a, b, c, and d are real numbers. Find [tex]a/c.

Question

Please help. 24 points!!

The inverse of
`f(x) = (2x-1)/(x+5)` may be written in the form
`f^(-1)(x)=(ax+b)/(cx+d)[]/tex, where a, b, c, and d are real numbers. Find [tex]a/c`.

Answer 1

The given function is,

`f(x)= (2x-1)/(x+5)`.

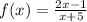Or,
`y= (2x-1)/(x+5)`

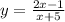
To find the inverse of a function, first step is to switch x and y. Therefore,

`x= (2y-1)/(y+5)`

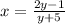
Next stpe is to solve the above equation for y t get the inverse f f(x). Hence, multiply each sides by y + 5 to get rid of fraction form. So,

`x*(y+5)= (2y-1)/(y+5)*(y+5)`

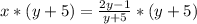
xy + 5x = 2y - 1

xy = 2y - 1 - 5x Subtract 5x from each sides to isolate y.

xy - 2y = -5x - 1 Subtract 2y from each sides.

y(x - 2) = -5x -1 Take out the common factor y.

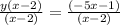`(y(x-2))/((x-2)) =((-5x-1))/((x-2))` Divide each sides by x-2.

`y=((-5x-1))/((x-2))`

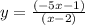
So,
`f^-1(x)=(-5x-1)/(x-2)`

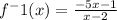
Now when we will compare
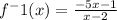`f^-1(x)=(-5x-1)/(x-2)` with
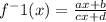`f^-1(x)=(ax+b)/(cx+d)` then we will get a = -5, b = -1, c = 1 and d=-2

So,
`(a)/(c) =(-5)/(1) =-5`

Hope this helps you!