Question

A flat (unbanked) curve on a highway has a radius of 170.0 m. a car rounds the curve at a speed of 25.0 m>s. (a) what is the minimum coefficient of static friction that will prevent sliding? (b) suppose that the highway is icy and the coefficient of static friction between the tires and pavement is only one-third of what you found in part (a). what should be the maximum speed of the car so that it can round the curve safely?

Answer 1

Step-by-step explanation:

Radius of the curve, r = 170 m

Speed of the car, v = 25 m/s

(a) Let
`\mu` is the coefficient of static friction that will prevent sliding. The centripetal force is balanced by the force of static friction as :

`(mv^2)/(r)=\mu mg`

`\mu=(v^2)/(rg)`

`\mu=((25)^2)/(170* 9.8)`

`\mu=0.375`

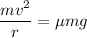
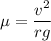
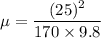
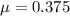
(b) Let v' is the maximum speed of the car so that it can round the curve safely if the coefficient of static friction between the tires and pavement is only one-third of what you found in part (a).

It is calculated as :

`v'=\sqrt{(1)/(3)\mu rg}`

`v'=\sqrt{(1)/(3)* 0.375* 170* 9.8}`

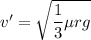
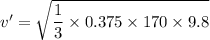
v' = 14.43 m/s

Hence, this is the required solution.