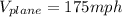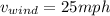Question

A plane flies 1800 miles in 9 ​hours, with a tailwind all the way. the return trip on the same​ route, now with a​ headwind, takes 12 hours. assuming both remain​ constant, find the speed of the plane and the speed of the wind.​ [hint: if x is the​ plane's speed and y the wind speed​ (in mph), then the plane travels to its destination at xplusy mph because the plane and the wind go in the same​ direction; on the return​ trip, the plane travels at xminusy ​mph.]

Answer 1

Initially its moving with tail wind so here the speed of wind will support the motion of the plane

so we can say

`V_(plane) + v_(wind) = (distance)/(time)`

`V_(plane) + v_(wind) = (1800)/(9)`

`V_(plane) + v_(wind) = 200 mph`

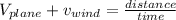
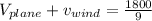
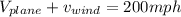
now when its moving with head wind we can say that wind is opposite to the motion of the plane

`V_(plane) - v_(wind) = (distance)/(time)`

`V_(plane) - v_(wind) = (1800)/(12)`

`V_(plane) - v_(wind) = 150mph`

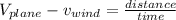
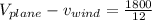
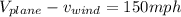
now by using above two equations we can find speed of palne as well as speed of wind

`V_(plane) = 175 mph`

`v_(wind) = 25 mph`