Question

A 700-turn circular coil with an area of 0.0550 m2 is mounted on a rotating frame that turns at a rate of 16.0 rad/s in the presence of a 0.0500-t uniform magnetic field that is perpendicular to the axis of rotation. what is the instantaneous emf in the coil at the moment that the normal to its plane is at a 30.0° angle to the field?

Answer 1

As per Faraday's law induced EMF is calculated by rate of change in flux

`EMF = N(d\phi)/(dt)`

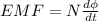
here magnetic flux is given by

`\phi = B.A = BAcos(wt)`

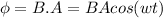
here w = angular speed of rotation

now we will use above faraday's law to find induced EMF

`EMF = N(d(BAcoswt))/(dt)`

`EMF = NBAw sin(wt)`

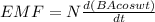
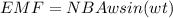
here

N = 700

A = 0.0550 m^2

B = 0.05 T

w = 16 rad/s

wt = 30 degree

`EMF = 700* 0.0550* 0.05* 16 * sin30`

`EMF = 30.8 Volts`

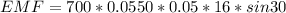
So induced EMF in the coil will be 30.8 Volts