Question

What is the measure of angle R shown below, given r = 10, q = 20, and Q = 100°? Round the answer to the nearest tenth.0.5° 2.0° 29.5° 50.5°

Answer 1

C

Explanation:

Edge 2020 present

Answer 2

Answer : 29.5°

Given r = 10, q = 20, and Q = 100°

From the attached figure we can see that two sides and one angle is given

We use sine rule to find angle R

`(sin A)/(a) = (Sin B)/(b) = (Sin C)/(c)`

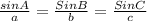
In triangle QRS

`(sin Q)/(q) = (Sin R)/(r) = (Sin S)/(s)`

r = 10, q = 20, and Q = 100°

`(sin Q)/(q) = (Sin R)/(r)`

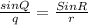
Replace all the values

`(sin 100)/(20) = (sin R)/(10)`

`(sin(100)*10)/(20) = sin(R)`

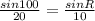
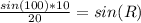
`(0.984807753*10)/(20)` =sin R

0.4932403876 = sin (R)

R=
`sin^(-1) (0.4932403876)`

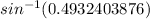
R= 29.5 degrees