Question

What is the orthocenter of a triangle with vertices A(−3,−2)A(−3,−2), B(−2,2)B(−2,2), and C(2,−2)C(2,−2)?

Answer 1

A(−3,−2), B(−2,2), C(2,−2)

The orthocenter is the meet of the altitudes. We see AC is parallel to the x axis so the perpendicular
`x=-2` is the altitude through B.

Between A and B we have slope (2 - -2)/(-2 - -3) = 4 so perpendicular slope -1/4 through C(2,-2):

`y+2 = -\frac 1 4 (x - 2)`

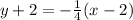
For the y coordinate of the orthocenter we substitute in x=-2.

`y+2 = -\frac 1 4(-2 - 2) = 1`

`y = -1`

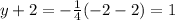
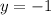
So the orthocenter is (x,y)=(-2,-1)

Answer: (-2,-1)