The equation of a parabola given

We have to write it in vertex form.
The vertex form of a parabola is
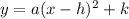
So to write it in vertex form we have to make the right side as a perfect square by using completing the square method.

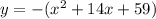
Here 14x given. By dividing 14 by 2 we will get 7. So we have to add and subtract
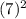 to the right side.
to the right side.
![y= -[x^2+14x+(7)^2-(7)^2+59]](https://img.qammunity.org/2019/formulas/mathematics/college/y2bysxpelf3zil23o099acnqzme6fy5gmx.png)
![y=-[x^2+14x+(7)^2-49+59]](https://img.qammunity.org/2019/formulas/mathematics/college/9itn5unv5eh1t25rnpqoc2u1mwvtdeiapz.png)
We know that,
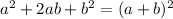 , so
, so
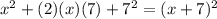 .
.
![y= -[(x+7)^2-49+59]](https://img.qammunity.org/2019/formulas/mathematics/college/2ogbdq7uz18zq6xrkajoft19l9zcdj5kyp.png)
![y=-[(x+7)^2 +10]](https://img.qammunity.org/2019/formulas/mathematics/college/5nh50jsfienxjm603aehen0d8zcqdra8jd.png)
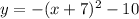
So we have got the required vertex form of the parabola.