Since ABC is equilateral, all 3 sides have equal length. side AC is 8 units since side BC is 8 units.
Line BD is placed in the middle, making D the midpoint of side AC.
knowing this information we can determine that the length of DC is 4 units (half of AC)
since triangle BDC is a right triangle, we can use the side lengths in the pythagorean theorem to find the length of BD
a²+b²=c² where a & b = legs of triangle , and c= hypotenuse (longest side)
we are given the hypotenuse and found one leg so we can plug our values into the equation to find the third
4² + b²= 8²
16 + b² = 64
b² = 48
b =
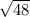
b= 4√3 or about 6.928 units
hope this helped