Question

E^2x - e^x - 6 = 0 (solve exponential equation(

Answer 1

Let's assume,
`e^x = y.`

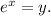
Hence, the given equation can be written as:

y² - y - 6 = 0

Next step is to factor the trinomial. For that, break down the constant -6 into two multiples so that their addition will result the coefficient of y =-1.

So, 6 = -3* 2

And sum of -3 and 2 will give -1.

Therefore, we can replace -y with -3y + 2y. So,

y² - 3y + 2y - 6 =0

(y² - 3y) + (2y - 6) =0 Make the group of terms.

y(y - 3)+ 2(y -3) =0 Take out the common factor from each group.

(y - 3 ) (y + 2) = 0 Take out the common factor (y - 3).

So, y - 3 = 0 and y + 2 =0 Equate both factor equal to 0.

Hence, y = 3 and -2.

So,
`e^x = 3 , e^x=-2`

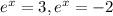
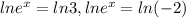`lne^x =ln 3 , lne^x=ln(-2)` Taking ln to each sides.

So, x = ln 3

But ln (-2) is not defined.

So, x = ln (3) is the real solution of the given equation.