Let the coordinates of the circumcentre O of the triangle DEF be (x, y). Circumcentre of a triangle is equidistant from each of the vertices.
1. Distance OD=distance OE, then:
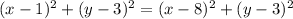 .
.
2. Distance OD=distance OE, then:
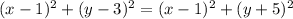 .
.
Solve the system:
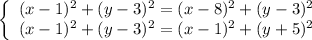 ,
,
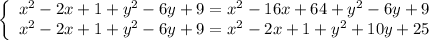 ,
,
 .
.
Then
 .
.
Answer: the coordinates of the circumcenter for ∆DEF are x=4.5, y=-1.