Since
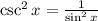 and
and
 , we can rewrite the right side of the equation as
, we can rewrite the right side of the equation as
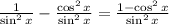
Using the identity
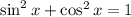 , we can subtract
, we can subtract
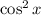 from either side to obtain the identity
from either side to obtain the identity
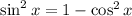
substituting that into our previous expression, the right side of our equation simply becomes
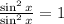
We can now write our whole equation as
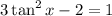
Adding 2 to both sides:
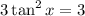
dividing both sides by 3:
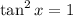
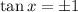
When 0 ≤ x ≤ π, tan x can only be equal to 1 when sin x = cos x, which happens at x = π/4, and it can only be equal to -1 when -sin x = cos x, which happens at x = 3π/4