Question

Please help i'm not that good at math. Determine the number of real solutions for each system of equations.

System A has blank
real solutions.

System B has blank
real solutions.

System C has blank
real solutions.

Answer 1

System A has ONE real solution

System B has NO real solutions

System C has ONE real solution

Answer 2

A is a circle around the origin and a line through the origin, so they'll intersect in two places; we can skip the detailed calculation.

B is the intersection of a parabola and a line; they can intersect in zero, one or two places depending on the details. Let's check

`y=x^2-7x+10=-6x+5`

`x^2-x+5= 0`

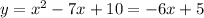
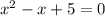
Discriminant,

`d = b^2-4ac=1-(4)(5)=-19`

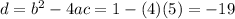
Negative discriminant, zero real solutions for B.

System C is again a parabola and a line; we proceed similarly:

`y = 8x+17 = -2x^2+9`

`2x^2+8x+8=0`

`x^2 + 4x + 4 = 0`

`d=b^2-4ac=16 - 4(1)(4)=0`

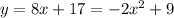
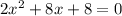
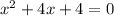
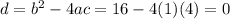
Zero discriminant, exactly one real solution for C.