Question

Which equation below represents the inverse function

Answer 1

Given function is
`a(b)=10*(b+7)/(2)`

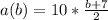
Or,
`a=10*(b+7)/(2)`

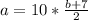
First step is to find the inverse is switch a and b. Therefore, the above equation will be:

`b=10*(a+7)/(2)`

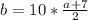
b = 5*(a + 7) By simplifying.

b = 5a + 35

Next step is to solve the equation for a to get the inverse of a (b). So, subtract 35 from each sides to isolate a. Hence,

b - 35 = 5a

`(b-35)/(5) =(5a)/(5)`

`(b)/(5) -(35)/(5)=a`

`(b)/(5) - 7 = a`

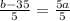
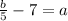
Therefore , the inverse is
`b(a)=(a)/(5) - 7`.

So, c is the correct choice.