Question

Boc= 90-1/2 angle bac
How to prove this ?

Answer 1

Alright, lets get started.

Please refer the diagram, I have attached.

∠ABC is given as y.

So, the ∠EBC will be 180 - ∠ABC.

∠EBC = 180 - y

As given in question, BO is the bisector of ∠EBC, it means ∠OBC will be half of the ∠EBC.

∠OBC =
`(1)/(2)` of ∠EBC

∠OBC =
`(1)/(2)` (180 - y)

∠OBC =
`90 - (y)/(2)`

Similarly,

the ∠DCB will be 180 - ∠ACB

∠DCB = 180 - z

As given in question, CO is the bisector of ∠DCB, it means ∠OCB will be half of the ∠DCB.

∠OCB =
`(1)/(2)` of ∠DCB

∠OCB =
`(1)/(2)` (180 - z)

∠OCB =
`90 - (z)/(2)`

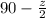
In triangle OBC, the sum of the angles of the triangle will be 180.

∠BOC +
`90 - (y)/(2)` +
`90 - (z)/(2)` = 180

∠BOC +
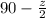`180 - (y)/(2) - (z)/(2) = 180`

∠BOC =
`(y)/(2) + (z)/(2)` =
`(y+z)/(2)`

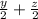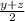
As per upper triangle ABC,
`x + y + z = 180`

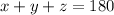
or
`y + z = 180 - x`

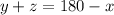
Putting this value in value of ∠BOC

∠BOC =
`(180-x)/(2)`

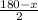
∠BOC =
`90 - (x)/(2)`

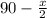
∠BOC = 90 -
`(1)/(2) BAC` : Hence proved

Hope it will help :)