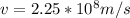As we know that refractive index of any medium with respect to vacuum is defined as
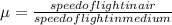
now its given that refractive index of vacuum with respect to glass is 2/3
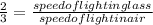
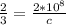
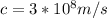
Part (ii)
Now similarly we have
refractive index of water with respect to vacuum is 4/3
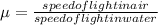
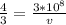
now we will have