Alright, lets get started.
The curve circle is given as
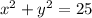
We could find the slope by diffentiating it.
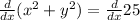
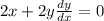

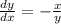
We hve given the point (3,-4). Putting its value as (x,y)
 = m
= m
The equation of line is y = mx + c
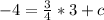

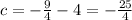
Putting the value of m and c in equation, Hence the eqution will be
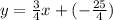
Multiplying the complete equation with 4
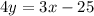
or
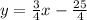
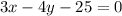 : Answer
: Answer
Hope it will help :)