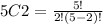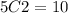Question

Act a bin contains 100 style a notebooks, 100 style b notebooks, and 100 style c notebooks. antoine will select 3 notebooks from the bin. how many different selections of 3 notebook styles are possible?

Answer 1

There are 10 different selections of 3 notebook styles are possible.

We can answer the question with the combinations formula.

First we determine that Antonie has to select 3 notebooks from 3 different styles (a,b,c).

We generally denote Combinations with nCk.

However, when we need to select 'k' number of item from 'n' styles, the formula changes to:

`(n+k-1)C(k-1)`

Substituting the values from the question in the equation we have,

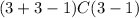`(3+3-1)C(3-1)`, which gives us

`5C2`

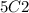
Now, we use the combinations formula to arrive at the final answer.

`nCr = (n!)/(r!(n-r)!)`

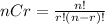
Substituting the values from above in the equation we have,

`5C2 = (5!)/(2!(5-2)!)`

`5C2 = 10`