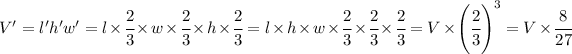Question

The length, width, and height of a right rectangular prism are multiplied by 23. What will be the effect on the volume of the prism?

The volume is multiplied by 2/3.
The volume is multiplied by 8/27.
The volume is multiplied by 4/9.
The volume is multiplied by 3/2.

Answer 1

Since none of the options make sense with 23, I assume it was a typo, and you meant 2/3.

Let l,w and h be the length, width and height of the original prism, and l',w' and h' be the length, width and height of the new prism. We are given

`l' = l* \cfrac{2}{3},\quad w' = w* \cfrac{2}{3},\quad h' = h* \cfrac{2}{3}`

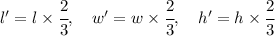
Also, if we call V the original volume, and V' the volume of the new prism, we have

`V = lhw,\quad V'=l'h'w'`

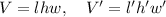
Substitute the expressions for l', h' and w' in the formula for V':

`V'=l'h'w' = l* \cfrac{2}{3}* w* \cfrac{2}{3}* h* \cfrac{2}{3} = l* h * w * \cfrac{2}{3}*\cfrac{2}{3}*\cfrac{2}{3} = V * \left(\cfrac{2}{3}\right)^3 = V*\cfrac{8}{27}`