The equation of motion of a particle is given by,
s =
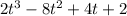
Let velocity of particle is denoted by v.
The velocity of the particle is given by,
velocity (v) =
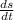
v =
![(d)/(dt) [ 2t^(3) - 8t^(2) + 4t +2 ]](https://img.qammunity.org/2019/formulas/physics/college/oy3u7rgc0lx6kojh3siu2tdi21fm54h61i.png)
v =
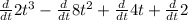
v =
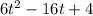
Thus, Velocity of particle is given by,
v =
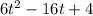
Let acceleration of the particle is denoted by a.
The acceleration of particle is given by,
Acceleration =
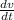
a =
![(d)/(dt) [6t^(2) -16t +4]](https://img.qammunity.org/2019/formulas/physics/college/14tyt5d3y2q822ldvyv5grht0cbv1b0hvm.png)
a =
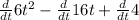
a = 12t - 16
Thus, acceleration of the particle is given by,
a = 12t - 16