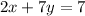Equation of a line given

We have to find an equation of a line which is perpendicular to the given line.
If the general equation of a line is
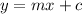 , m is the slope of the line there. And the slope of the perpendicular line will be the negative reciprocal of m which is
, m is the slope of the line there. And the slope of the perpendicular line will be the negative reciprocal of m which is
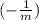 .
.
So first here we have to make the given equation as
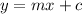

First we have to move 7x to the right side by subtracting it from both sides.
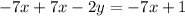

Now to get y we have to move -2, by dividing it on both sides.
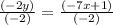
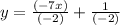
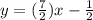
So here the slope
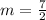
Now the slope for the perpendicular equation is
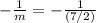
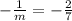
So slope of the perpendicular line is

We can write the perpendicular equation as

Now this equation is passing through the point (-4,5)
We have to plug in x = -4 and y = 5 in the line to get c.
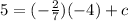
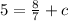

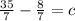
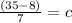
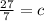
So we have got the value of c. Now we can write the perpendicular equation as,
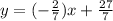
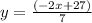
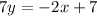

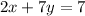
So we have got the required perpendicular line.
The equation of the perpendicular line is