Given
A person counted 60 steps going up an up-escalator, and 90 steps going down the same up-escalator.
Find
The number of steps she would count if the escalator were standing still.
Solution
This is perhaps the long way around, but we get there.
Define the following variables:

The rate at which the steps of the distance d are traversed is w+e (going up) or w-e (going down). The number of steps counted is the rate at which steps are walked (w) multiplied by the time spent going up or down. We can write 4 equations in the 5 unknowns.

Dividing the second by the first, we have

Equating the third and 4th equations, and substituting for td, we have
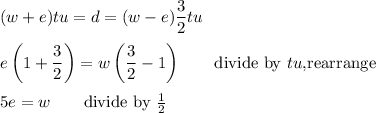
Solving the first equation for tu and substituting into the third equation, we get
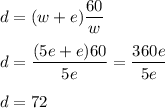
The number of steps between floors is 72, which is the number she would count if the escalator were not moving.