The logarithmic expression is
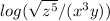
To expand the expression we have to use some properties of logarithm.
We know that
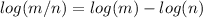
By using this property we can write,
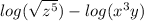
Square root means to the power 1/2, so for
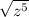 , we can write
, we can write
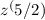 .
.
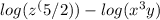
Now we have to use another property of logarithm.
We know that,
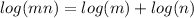
So we will use this property to
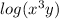
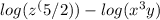
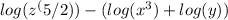
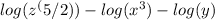
Now we have to use another property of logarithm.
We know that,
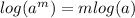
By using this property we can write,
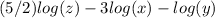
This is the required aswer here.