We are given
length of sides are
AB=7
AC=7
BC=6
now, we can use formula of area of triangle
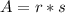
where
A is area of triangle
r is radius of in-circle
s is semi-perimeter of triangle
step-1: Finding area of triangle
We can use
Heron's formula
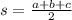
a , b and c are values of sides
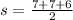


now, we can plug values
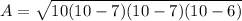
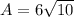
step-2: Finding radius(r)
we got
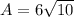

now, we can find radius
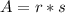
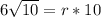
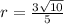 ............Answer
............Answer