The given geometric sequence is 3, 12, 48, 192, ....
The first term (a) = 3
The common ratio is the factor between the terms. we can get it by dividing the second term by the first term or third term by the second term and so on.
The common ratio (r) = 12/3 = 48/12 = 192/48 = 4
The formula to get the geometric sequence is
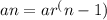
We will have to plug in the values of a and r here.
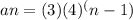
So we have got the required geometric sequence.
The correct option is c.