Answer for question (42):
We need to find the composition of two functions f(x) and g(x).
By the definition, the composition of two functions
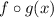 is defined as
is defined as
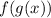 .
.
That is, The composition of two functions f and g is the new function , by performing g first and then performing f.
Here we have
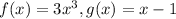
![f\circ g(x)=f[g(x)]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/zlexnfmdciwylhvyorfe3zhgq89392eh49.png)
Now plug in
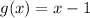 , we get
, we get
![f\circ g(x)=f[g(x)]=f(x-1)](https://img.qammunity.org/2019/formulas/mathematics/middle-school/xarsby2r5x4iqnvjc5ep02s9q90xspriei.png)
It is given that
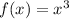 , using this we need to find
, using this we need to find
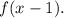
Replace x by x-1 in f(x),
![f[g(x)]=f(x-1)=3(x-1)^3](https://img.qammunity.org/2019/formulas/mathematics/middle-school/c4asx0390k93p0j3j1ymzlawt97p7clw14.png)
Now we need to find
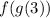 ,
,
![f[g(3)]=3(3-1)^3=3(2^3)=3*8=24](https://img.qammunity.org/2019/formulas/mathematics/middle-school/9bjhrmih7bivlbcwmpj5bhjg61058enk07.png)
So

So the soiution is (B): 24
Solution for question (43):
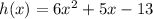
Plug in
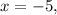 to find h(-5):
to find h(-5):
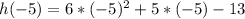
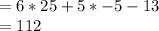 +5(-5)-13 [/tex]
+5(-5)-13 [/tex]
Thus the answer for (43) is (D): 112.
Solution for question (44):
The height of a ball projected into the air can be represented by the function is
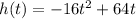
Then to find the height of the ball in feet when it has been in the air for 2 seconds:
Plug in t=2 in h(t),
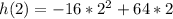
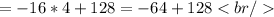
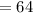
Thus the answer for (44) is (A): 64.