Question

Cleopatra uploaded a funny vat video on her website, which rapidly gains views over time. The relationship between the elaspsed time,t, in days, since Cleopatra uploaded the video, and the total number of views, V(t), is modeled by the following function: Vday(t) = 580 • (1.17)^t . Every week, the number of views grows by a factor of what?

Answer 1

every week, the number of views grows by a factor of 3

Explanation:

Answer 2

The function given to us is:

`V(t) = 580(1.17)^t`

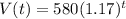
where
`t` is in days.

We know that the number of days in a week is 7.

Thus, to find out by what factor does the number of views grow in a week all that we have to do is realize that the starting of any week will have the expression as:

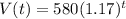`V(t) = 580(1.17)^t`..................(Equation 1)

and the end of the week will have the expression as:

`V(t+7) = 580(1.17)^(t+7)`..................(Equation 2)

And so to find the growth factor in a week, we will have to divide (Equation 2) by (Equation 1), which yields:

`(V(t+7))/(V(t))=(580(1.17)^(t+7))/(580(1.17)^(t))=((1.17)^t* (1.17)^7)/((1.17)^t)`

`\therefore (V(t+7))/(V(t))=(1.17)^7\approx3`

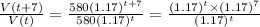
Thus, the number of views grow by a factor of 3 in a week.