Question

Solve For Each Variable.

1. 6 = 1 - 2n + 5

2. 8x - 2 = - 9 + 7 x

3. - 8 = - ( x + 4 )

Answer 1

The first equation given
`6=1-2n+5`

We have to add 1 and 5 to the right side first. We will get,

`6= 6 - 2n`

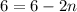
To get rid of 6 from the right side we have to subtract 6 from both sides.

`6-6 = 6-6-2n`

`6-6 = -2n`

`0=-2n`

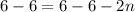
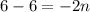
To find n we have to move -2 to the other side by dividing both side by -2.

`0/-2 = -2n/-2`

`0= n`

`n=0`

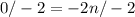
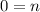
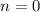
So we have got the required answer for the first question.

The solution is n = 0.

The second equation given,

`8x-2 = -9+7x`

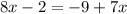
First we have to move 7x to the left side by subtracting it from both sides.

`8x-7x-2 = -9+7x-7x`

`8x-7x-2 = -9`

`x-2 = -9`

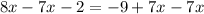
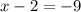
Now we have to move -2 to the right side by adding 2 to both sides.

`x-2+2 = -9+2`

`x = -9+2`

`x = -7`

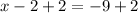
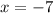
We have got the required answer for the second question.

The solution is x = -7.

The third equation given,

`-8 = -(x+4)`

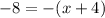
We have to get rid of that negative sign from both sides. As we have negative sign to both sides we can cancel it out. We will get,

`8=x+4`

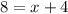
Now we have to move 4 to left side by subtracting it from both sides.

`8-4 = x+4-4`

`8-4 = x`

`4=x`

`x = 4`

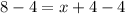
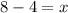
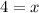
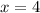
So we have got the required answer .

The solution is x = 4.