Question

Find an equation of the line having the given slope 2/3 and containing the given point (7,-8)

Answer 1

Hi!

I'll be looking for point slope form, or y -
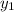`y_(1)` = m (x -
`x_(1)`), with m being the slope,
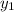`y_(1)` being the y coordinate of any given point on the line, and
`x_(1)` being the x coordinate of that same point.

So in this case, we're given the x coordinate of 7 and the y of -8, as well as a slope of 2/3. So if you substitute that in, you get:

y - (-8) = 2/3 (x - 7)

y + 8 = 2/3 (x - 7)

If you wanted to convert that to slope intercept form, just distribute the 2/3.

y + 8 = 2/3 (x - 7)

y + 8 = 2/3x - 14/3

y = 2/3x - 38/3

Now to standard form:

-2/3x + y = -38/3

Divide everything by -1

2/3x - y = 38/3

You can use any of those 3 solutions.

Hope this helped!

Answer 2

To begin, we should use our given information to write the equation of a line in point-slope form, y = m(x-h) + k, where the variable m represents the slope and the point (h,k) is on the line. Substitution of these values is modeled below:

y = m(x-h) + k

y = 2/3(x - 7) - 8

Next, we should use the distributive property to multiply the 2/3 by the values inside the parentheses. We should also convert the constant -8 into thirds for simpler computation.

y = 2/3x - 14/3 - 24/3

Finally, we should perform the subtraction of the constants.

y = 2/3x - 38/3

Therefore, your answer is y = 2/3x - 38/3.

Hope this helps!