Question

The graph represents the function f(x) = 10(2)^x.

How would the graph change if the b value in the equation is decreased but remains greater than 1? Check all that apply.

Answer 1

Option C and D.

Explanation:

The given function is

`f(x)=10(2)^x`

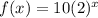
The general exponential function is

`g(x)=a(b)^x`

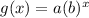
where, a is initial value and b is growth factor.

If b>1, then g(x) is an increasing function.

If 0<b<1, then g(x) is an decreasing function.

On comparing both equation we get a=10 and b=2.

The b value in the equation is decreased but remains greater than 1.

1 < b < 2

Let b=1.5, So, the given function will

`f(x)=10(1.5)^x`

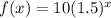
At x=0

`f(x)=10(1.5)^0=10(1)=10`

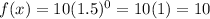
It means the y-intercept of new function is 10.

Since b>1, therefore the y-values will continue to increase as x-increases.

1.5 < 2, it means the graph will increase at slower rate.

Thus, the correct options are C and D.

Answer 2

Consider the graph of the function
`y=10\cdot b^x`, where
`1<b<2`.

1. For
`1<b<2` you have that
`b^0=1` and
`10\cdot b^0=10\cdot 1=10`. This means that point (0,10) is y-intercept of this graph (the same as for function
`y=10\cdot 2^x`).

2. For
`1<b<2` you have that
`b^x<2^x`, then
`10 \cdot b^x<10\cdot 2^x` and function is increasing. This means that the graph will increase at a slower rate and y-values will continue to increase as x-increases.

3. Not all y-values will be less than their corresponding x-values. For example, when b=1.5 and x=2,

`y=10\cdot 1.5^2=22.5`.

As you can see x<y.

Answer: correct options are C and D, incorrect - A, B and E.