Question

Identify the quadratic function(s). (Select all that apply.)

A)8 - 5x = 4(3x - 1)
B)(4a + 2)(2a - 1) + 1 = 0
C)2y + 2(3y - 5) = 0
D)2b(b - 7) + b = 0

Answer 1

B and D are the answers

Explanation:

Simple and short. If you want the working see the answer before mine.

Answer 2

General Idea:

The quadratic function of the form
`ax^2+bx+c=0`.

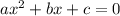Applying the concept:

Simplifying the equation in option A, we get...

`A) \; 8 - 5x = 4(3x - 1) \\Distributing \; 4 \; in \; right \; side \; of \; the \; equation. \\ \\ 8 - 5x = 12x - 4\\ The \; equation \; is \; a \; linear \; equation \; with \; variable \; on \; both \; sides.`

Simplifying the equation in option B, we get...

`B) \; \; (4a + 2)(2a - 1) + 1 = 0\\ Multiplying \; First \; \; Outer \; \; Inner \; \; Last \; terms\; in\; the \; left \; side.\\ \\ 4a \cdot 2a + 4a \cdot -1 + 2 \cdot 2a + 2 \cdot -1 + 1 = 0\\ \\ 8a^2-4a+4a-2+1=0\\ Combining \; like \; terms \; \\ \\ 8a^2 - 1 = 0\\ Above \; is \; a \; Quadratic \; Equation!`

Simplifying the equation in Option C, we get...

`C)\; \; 2y + 2(3y - 5) = 0\\ Distributing \; 2 \; in \; left \; side\\ \\ 2y+6y-10=0\\ Combining \; like \; terms\\ \\ 8y - 10 = 0\\ Above \; Equation \; is \; linear \; equation`

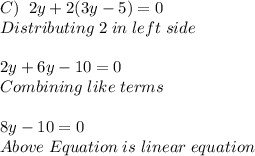
Simplifying the equation in Option D, we get

`D) \;2b(b - 7) + b = 0\\ Distributing \; 2b\; in \;the \;left\; side \;of \;the\;equation\\ \\ 2b \cdot b - 2b \cdot 7+b=0\\ Simplify \; in \; the \; left \; side \; of \; the \; equation\\ \\ 2b^2-14b+b=0\\ Combine \; like \; terms\\ \\ 2b^2-13b=0\\ Above \; equation \;is \;a \; Quadratic\;Equation!`

Conclusion:

Option B) & Option D) are quadratic equation!