Question

If a windshield wiper covers an area of approximately 160 square inches when it rotates at an angle of 84°, find the length of the wiper to the nearest tenth of an inch.

Answer 1

General Idea:

We can use the below formula to find the area of sector (A), when angle of sector and radius is given:

`A=(\theta)/(360) \cdot \pi \cdot r^2`

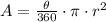
Applying the concept:

We need to substitute 84 for
`\theta` and 160 for A in the above formula:

`160 = (84)/(360) \cdot \pi \cdot r^2\\ Solving \; for \; r\\ \\ (84\pi)/(360) \cdot r^2=160\\ Multiply \; the \;reciprocal\; (360)/(84\pi) \;on\;both\;sides\;of\;the\;equation\\ \\ r^2=160\cdot (360)/(84\pi) \\ \\ r^2=(57600)/(84\pi) \\Taking \;square\;root\;on\;both\;sides\\ r=\sqrt{(57600)/(84\pi)} \approx14.8\; inch`

Conclusion:

If a windshield wiper covers an area of approximately 160 square inches when it rotates at an angle of 84°, the length of the wiper to the nearest tenth of an inch is 14.8