Isolate the radical term, then square both sides:
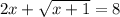
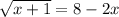
Note that
 is non-negative and requires that
is non-negative and requires that
 in order to be defined, while
in order to be defined, while
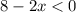 when
when
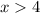 . This means we can only find real solutions in the range
. This means we can only find real solutions in the range
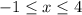 .
.
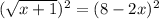
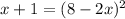
Now just expand the RHS and simplify as much as possible:
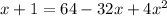
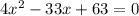
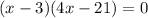
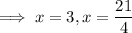
Now,
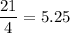 , which is larger than 4, so we omit that solution. Then
, which is larger than 4, so we omit that solution. Then
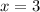 is the only solution.
is the only solution.