Question

GEOMETRIA- EQUAÇÕES E RELAÇÕES FUNDAMETAIS

Answer 1

I have a Portuguese Water Dog who's translating for me.

a.

`\sin x + \cos x = -1`

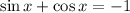
Usually I'll say the linear combination of a sine and a cosine of the same angle is a phase shift and a dilation etc. but here we can take a shortcut. The only time we'll get -1 as the sum is when one of the terms is -1, then the other term will be zero because of
`\cos^2 x + \sin ^2 x = 1`.

`\sin x = -1 \textrm{ or } \cos x = -1`

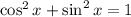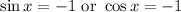
Answer: x = 3π/2 or x=π

b.

`\cos x = \frac 1 2`

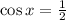
That's the biggest cliche of trig 30/60/90 so x=plus or minus 60 degrees. We're told we're in the fourth quadrant, so

`\sin x = - (√(3))/(2)`

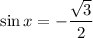
Answer: -√3/2

c.

This time we're in the third quadrant, negative sine

`\cos^2 x + \sin ^2 x = 1`

`\cos x = - √( 1- \sin ^2 x) = -√(1 - (-3/4)^2) = -√(1-9/16) = -√(7/16) = -\frac 1 4 \sqrt 7`

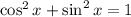
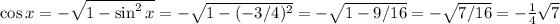
Answer: -(1/4)√7

d.

Second quadrant positive sine, negative tangent

`\sin x = √(1 - \cos^2x) = \sqrt{ 1 - (-3 √(2)/5)^2} = √(1 - 18/25)=\frac 1 5 √(7)`

`\tan x = (\sin x)/(\cos x) = (√(7)/5 )/(-3 √(2) / 5) = -(√(14))/(6)`

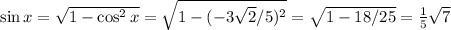
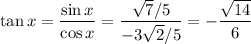
Answer: sin x = √7/5, tan x = -√14/6

e.

We're given the tangent and the sine

`\tan x = (\sin x )/(\cos x)`

`\cos x = (\sin x )/(\tan x ) = (√(5)/5)/(-1/2) = - \frac 2 5 √(5)`

Answer: (-2/5)√5