Question

What is the vertex of f(x)=-x2-6x

Answer 1

The vertex of the parabola is (-3, 9)

In order to find the vertex of any quadratic, you start by finding the x-value of said vertex. This can be done using the equation below.

-b/2a

In this equation 'a' refers to the coefficient of x^2 (-1) and 'b' refers to the coefficient of x (-6). So then we can plug into that equation using those values.

-b/2a

-(-6)/2(-1)

6/-2

-3

Now that we have the x value, we can substitute that value into the equation to find the y value.

f(x) = -x^2 - 6x

f(x) = -(-3)^2 - 6(-3)

f(x) = -(9) + 18

f(x) = 9

Therefore our point is (-3, 9)

Answer 2

We are given this quadratic equation :

`f(x) =-x^(2) -6x`

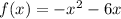
For a given equation of the form:

`f(x) =ax^(2) +bx +c`

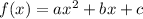
We can find the vertex (h,k), by first finding h of vertex by :

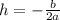`h=-(b)/(2a)`............(1)

and k(y-coordinate) can be found by plugging this x-value in the given equation.

Now if we compare our equation with the general form, we can find our a, b and c as :

a=-1 and b=-6 and c=0

so plugging these values in equation (1), to get x-coordinate as

`h=-(b)/(2a) = -(-6)/(2*(-1))`

`h=-(-6)/(-2) = -(6)/(2)`

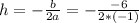
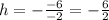
h=-3

Now plugging this value in the given equation to solve for x,

`f(x) = -((-3)^(2) ) -6(-3)`

`f(x) = -(9) -6(-3)`

`f(x) = -9 +18`

`f(x) = 9`

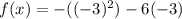
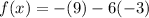
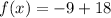
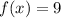
k=9

So vertex is (-3,9)