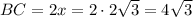Question

The "longer" leg of a 30-60-90 triangle is 6. what is the length of the hypotenuse?

Answer 1

Wouldn't the length of the hypothenuse be 6 since the hypotenuse is the longest side of a triangle?

Answer 2

A 30-60-90 triangle is half an equlateral triangle (refer to the image below).

If we call the length of the side
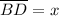`\overline{BD} = x`, we can see that it is exactly half of the side of the equilateral triangle. So, we have

`\overline{AB} = \overline{AC} = \overline{BC} = 2\cdot \overline{BD} = 2x`

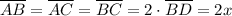
Moreover, we can find the height
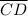`\overline{CD}` using the pythagorean theorem, having

`\overline{CD} = √(4x^2-x^2) = √(3x^2) = x√(3)`.

Now, you know the longer leg to be 6. The longer leg is the height, so you have

`\overline{CD} = x√(3) = 6 \implies x = \overline{BD} = \cfrac{6}{√(3)} = \cfrac{6√(3)}{3} = 2√(3)`

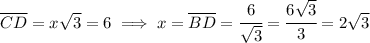
So, the hypotenuse is twice that value:

`BC = 2x = 2\cdot 2√(3) = 4√(3)`