Let's solve the sine equation.
1. Express sine function in the left side of equation:
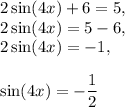 .
.
2. Use the genereal solution to get the solution of your equation:
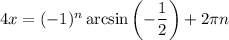 , where
, where
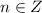 .
.
3. Find
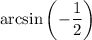 :
:
 .
.
4. Substitute part 3 into part 2 and express x:
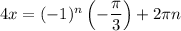 , where
, where
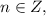
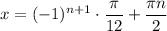 , where
, where
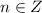 .
.
5. Solutions of your equation are:
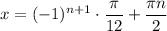 , where
, where
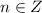 .
.