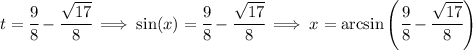Question

Use inverse functions where needed to find all solutions of the equation in the interval 2 cos2 x + 9 sin x = 6

Answer 1

You can use the identity
`\cos(2x) = \cos^2(x)-\sin^2(x)` to write the equation as

`2(\cos^2(x)-\sin^2(x))+ 9\sin(x) = 6`

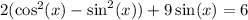
Now, from the fundamental equation of trigonometry, deduce an expression for
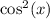`\cos^2(x)` in terms of
`\sin^2(x)`:

`\cos^2(x)+\sin^2(x) = 1 \implies \cos^2(x) = 1-\sin^2(x)`

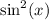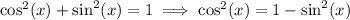
The equation becomes

`2(1-\sin^2(x)-\sin^2(x))+ 9\sin(x) = 6 \iff 2(1-2\sin^2(x))+ 9\sin(x) = 6`

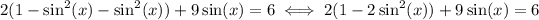
Simplify the left hand side and move all terms to left hand side:

`2-4\sin^2(x)+ 9\sin(x) -6 = 0 \iff -4\sin^2(x) + 9\sin(x) - 4 = 0`

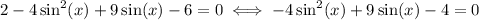
Now, if you let
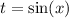`t = \sin(x)`, this equation becomes a quadratic equation:

`-4t^2 + 9t - 4 = 0`

The two solutions of this equations are

`t = \cfrac{9}{8} - \cfrac{√(17)}{8},\quad t = \cfrac{9}{8} + \cfrac{√(17)}{8}`

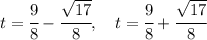
We must be careful, because we have to remember that
`t` was actually
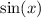`\sin(x)`. This means that
`t` can only assume values between -1 and 1. The second solution exceeds 1, so we reject it. So, we have

`t = \cfrac{9}{8} - \cfrac{√(17)}{8} \implies \sin(x) = \cfrac{9}{8} - \cfrac{√(17)}{8} \implies x = \arcsin\left(\cfrac{9}{8} - \cfrac{√(17)}{8}\right)`