we are given
equation of curve is
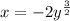
Bound is
from y=0 to y=9
now, we can use arc length formula
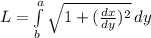
Firstly , we will find dx/dy
that is derivative
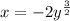

now, we can simplify it

Arc length:
now, we can plug it in arc length formula
and we get
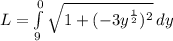
now, we can solve it
Firstly , we will solve integral

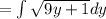
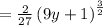
now, we can plug bounds
and we get
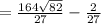
 ...........Answer
...........Answer