Question

What is the radius of the circle inscribed in triangle $abc$ if $ab = 5, ac=6, bc=7$? express your answer in simplest radical form?

Answer 1

General Idea:

There are two formula's to find the area of triangle when three sides are given.

FIRST FORMULA: When a, b and c are the three sides of the triangle, we can use the Heron's triangle to find the Area of triangle.

`Area \ of\ triangle =√(s(s-a)(s-b)(s-c)) ,\\\\ \ where\ s= (a+b+c)/(2)`

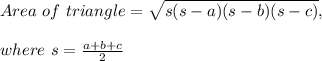
SECOND FORMULA: When the circle is inscribed in a triangle with radius r, then we can use the below formula to find the Area of triangle.

`Area\ of\ triangle=(1)/(2) \cdot(a+b+c)\cdot r`

Applying the concept:

In our problem we are given the side lengths of triangle as 5, 6, & 7

Area of triangle using first formula:

`s=(5+6+7)/(2)=(18)/(2)=9\\ \\ Area=√(9(9-5)(9-6)(9-7))=√(9(4)(3)(2)) \\\\Area=6√(6)\ square\ units.`

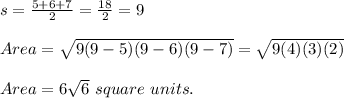
Area of triangle using second formula:

`Area=(1)/(2)\cdot (5+6+7)\cdot r\\ \\ Area=(1)/(2) \cdot(18)\cdot r\\ \\ Area =9r`

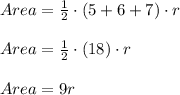
Conclusion:

We need to set up an equation based on the results that we get when finding the area of triangle using first and second formula, we get..

`image`

Answer 2

You can use the area method. First of all, find s that is half of perimeter:

`s=(5+7+6)/(2) =9` un.

Then:

1. Find the area of triangle using Heron's fofmula:

`A=√(9\cdot (9-5)\cdot (9-7)\cdot (9-6)) =√(9\cdot4 \cdot 2\cdot 3) =6√(6)` sq. un.

2. Find the area of triangle using the formula
`A=s\cdot r`, where r is the radius of inscribed circle.

`A=9\cdot r` sq. un.

3. Equate both expressions:

`6√(6) =9r,\\ r=(6√(6))/(9)=(2)/(3) √(6)` un.

Answer:
`r=(2)/(3) √(6)` un.