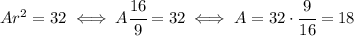Question

I need acellus help!

Answer 1

re-deduce the scale factor, the side of "12" inches is the result of multiplying the "9" inches factor by the scale factor. witch will give you (9r=12 <->r=12/9=3)

now we can gladly use the result about the areas: the area of the figure on the left, "a" , is given by:

(Ar^2=32)

(a 16/9=32)

a=32 X 9/16=18 "18"

I really hoped this helped xD

Answer 2

When two figures are similar, one is the scaled version of the other.

This means that all the correspondant sides of the two figures are in the same proportion, i.e. there exists a number
`r` such that every side of the figure on the right is computed by multiplying the correspondant side of the figure on the left by
`r`

If this is the case, the two areas are also proportional, but the coefficient is squared: this means that the area of the figure on the right is not
`r` times the area of the figure on the left, but rather
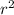`r^2` times.

We are given two correspondant sides, so we can deduce the scale factor: the side of 12 inches is the result of multiplying the 9 inches factor by the scale factor, so we have

`9r = 12 \iff r = \cfrac{12}{9} = \cfrac{4}{3}`.

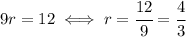Now let's use the result about the areas: the area of the figure on the left,
`A`, is given by

`Ar^2 = 32 \iff A \cfrac{16}{9} = 32 \iff A = 32\cdot \cfrac{9}{16} = 18`