Question

A factory tests a random sample of 30 transistors for defects. the probability that a particular transistor will be defective has been established by past experience as 0.04. what is the probability that there are no defective transistors in the​ sample?

Answer 1

The probability that there are no defective transistors in the sample is 41.2%.

Step-by-step explanation:

To find the probability that there are no defective transistors in the sample, we can use the binomial distribution. The probability of a particular transistor being defective is 0.04, so the probability of it not being defective is 1 - 0.04 = 0.96. The formula for calculating the probability of no defective transistors in a sample of size n is (0.96)^n. In this case, n = 30, so the probability is (0.96)^30 = 0.412, or 41.2%.

Answer 2

Let X be the number of defective transistors. Let p be the probability that defective transistor.

P(defective transistor) = 0.04

P(non defective ) = 1- 0.04 = 0.96

A random sample of size 30 is tested for defects and we want to find probability of no defective transistor

P(No defective transistor) = P(X= 0)

Here X follows binomial distribution with parameters n=30 and p=0.04

The Binomial probability function with parameters n and p is

P(X=x) =
`(nCx) p^(x) (1-p)^(n-x)`

P(X=0) =
`(nC0) p^(0) (1-p)^(n-0)`

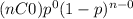
Using n=30 and p=0.04

P(X=0) =
`(30C0) 0.04^(0) (1-0.04)^(30-0)`

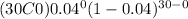
P(X=0) = 1*1*(0.96)^30

P(X=0) = 0.2938

The probability that there are no defective transistors in the sample is 0.2938