Answer:
Option A. -1023
Explanation:
If we form the finite geometric sequence by using expression
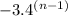 by putting n = 1, 2, 3, 4, 5.
by putting n = 1, 2, 3, 4, 5.
Sequence will be = -3, -12, -48, -192, -768
Now we can either do the total of all numbers of the sequence or use the formula to calculate the sum.
Total of terms = (-3) + (-12) + (-48) + (-192) + (-768) = -1023
Or by using formula
Sum =
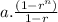
Here a = -3
r = (-12)/(-3) = 4
n = 5
Therefore sum of the sequence =

Option A is the answer.