Question

HELP ASAP

The distance traveled, in feet, of a ball dropped from a tall building is modeled by the equation d(t) = 16t2 where d equals the distance traveled at time t seconds and t equals the time in seconds. What does the average rate of change of d(t) from t = 2 to t = 5 represent?

A. The ball travels an average distance of 112 feet from 2 seconds to 5 seconds.
B. The ball falls down with an average speed of 48 feet per second from 2 seconds to 5 seconds.
C.The ball falls down with an average speed of 112 feet per second from 2 seconds to 5 seconds.
D. The ball travels an average distance of 48 feet from 2 seconds to 5 seconds.

Answer 1

The appropriate choice is ...

... C.The ball falls down with an average speed of 112 feet per second from 2 seconds to 5 seconds.

Explanation:

Answer 2

As with many math problems, there are at least a couple of ways you can work this.

1. Figure average rate of change in the usual way:

`(f(5)-f(2))/(5-2)=(400-(64))/(3)=(336)/(3)\\=112\quad\text{feet per second}`

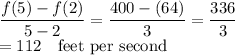
2. Realize that the downward speed is increasing at a constant rate (32 ft/s²), so the average speed on the interval will be the speed at the midpoint of the interval: t = (2+5)/2 = 3.5 seconds. Since the downward speed started from zero, at t=3.5, it is

(3.5 s)×(32 ft/s²) = 112 ft/s

_____

The appropriate choice is ...

... C.The ball falls down with an average speed of 112 feet per second from 2 seconds to 5 seconds.