Question

Solve the triangle.

A = 51°, b = 11, c = 7

a ≈ 12.8, C ≈ 39.1, B ≈ 89.9
a ≈ 8.5, C ≈ 39.1, B ≈ 89.9
No triangles possible
a ≈ 12.8, C ≈ 43.1, B ≈ 85.9

Answer 1

2

Explanation:

just took the test

Answer 2

For a better understanding of the solution provided here please find the attached diagram.

To find the answer to this question, we will have to use the Sine Rule and the trial and error method as the required number of variables are not known.

The Sine Rule is as:

`(Sin A)/(a)= (Sin B)/(b)=(Sin C)/(c)`

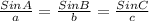
Plugging in all the values of the known variables we get:

`(Sin (51^0))/(a)= (Sin B)/(11)=(Sin C)/(7)`

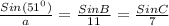
If we take the first two ratios, we get:

`(Sin (51^0))/(a)= (Sin B)/(11)`

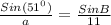
Which will give us:

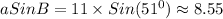`aSinB=11* Sin(51^0)\approx8.55`.............(Equation 1)

Likewise, if we take the first and the last ratio, we get:

`(Sin (51^0))/(a)= (Sin C)/(7)`

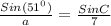
Which will give us:

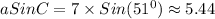`aSinC=7* Sin(51^0)\approx5.44`.............(Equation 2)

After applying trial and error to the given set of choices or options, we see that (Equation 1) is best satisfied by the Second Option. Obviously, the second option will have to satisfy (Equation 2) too. Let us see if the Second Option best satisfies both the equations.

In the second option, we are given that a ≈ 8.5, C ≈ 39.1, B ≈ 89.9

Plugging in the values on the Left Hand Side of (Equation 1), we get:

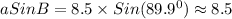`aSinB=8.5* Sin(89.9^0)\approx8.5` which is almost equal to the right hand side of (Equation 1).

Likewise, we can show that (Equation 2) is best described by the Second Option.

Thus, within the accepted error range, out of the given options, Second Option comes closest to being the solution of the triangle.