Question

Given this equation of a circle, x2 + y2 + 8x – 4y + 12 = 0. Using completing the square, identify the coordinates of the center of the circle. Also, give the length of the radius of the circle. Please include all work for full credit.

Answer 1

x² + y² + 8x - 4y + 12 = 0

Circle equation: (x - a)² + (y - b)² = r², so,

x² - 2.x.a + a² + y² - 2.y.b + b² - r² = 0

x² + y² - 2ax - 2by + a² + b² - r² = 0

-2ax = 8x

-2a = 8

a = 8/-2

a = -4

-2by = -4y

-2b = -4

b = -4/-2

b = 2

So, (x + 4)² + (y - 2)² - r² = 0

a² + b² - r² = 0

(-4)² + 2² = r²

16 + 4 = r²

r² = 20

So, after all:

(x + 4)² + (y - 2)² = 20

The coordinates of the center is always the opposite of a and b,

So, the center is (-4, 2)

And the radius is r² = 20 => r = √20 => r = 2√5

Answer 2

The coordinates of the center of the circle is: (-4,2)

The length of the radius of the circle is: 2√2

Explanation:

We know that the general equation of a circle i.e. the equation of a circle in square form is given by:

`(x-h)^2+(y-k)^2=r^2`

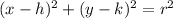
where (h,k) is the center of the circle and r is the radius of the circle.

The equation of the circle is given by:

`x^2+y^2+8x-4y+12=0`

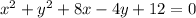
Now, on combining the terms of x and y we have:

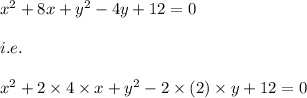
`x^2+8x+y^2-4y+12=0\\\\i.e.\\\\x^2+2* 4* x+y^2-2* (2)* y+12=0`

i.e.

`x^2+4^2-4^2+2* 4* x+y^2-(2)^2+(2)^2-2* 2* y+12=0\\\\i.e.\\\\x^2+4^2+2* 4* x-4^2+y^2-2^2+2^2-4y+12=0\\\\(x+4)^2+(y-2)^2-16-4+12=0\\\\i.e.\\\\(x+4)^2+(y-2)^2-8=0\\\\i.e.\\\\(x+4)^2+(y-2)^2=8`

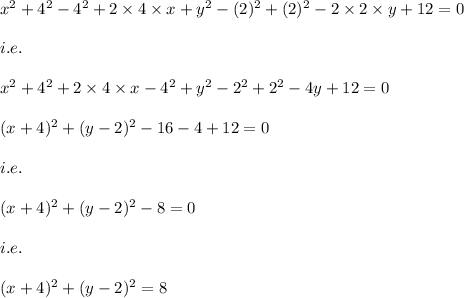
Hence, we get:

`(x-(-4))^2+(y-2)^2=(2√(2))^2`

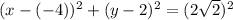
Hence, the center of the circle is: (-4,2)

and the radius of the circle is: 2√2